In der taktfeinen Umlegung wird grundsätzlich davon ausgegangen, dass Fahrgäste Takte und Fahrzeiten der Linien kennen.
Über welche Informationen sie darüber hinaus verfügen, ist entscheidend für ihr Wahlverhalten beim Ein- oder Umsteigen. Visum bietet dazu vier verschiedene Modelle an:
- Keine Information und exponentiell verteilte Takte
- Keine Information und konstante Takte
- Information über die verstrichene Wartezeit
- Information über die nächsten Abfahrtszeiten auf den Linien der Haltestelle
Welches Wahlmodell für die Umlegung verwendet wird hängt am eingestellten Fahrgastinformationslevel in den Parametern der taktfeinen Umlegung (Taktfeine Umlegung: Register Suche).
Im Folgenden werden die einzelnen Wahlmodelle für die Situation des an einer Haltestelle wartenden Fahrgastes vorgestellt. Zur Beschreibung der mathematischen Grundlagen benötigen wir noch einige Bezeichnungen.
Notation
L = {1, ..., n} bezeichne die Menge der verfügbaren Linien. Jede Linie i ∈ L hat eine gewisse Rest-Reisezeit si ≥ 0 und einen Takt hi > 0. Aus letzterem wird die Frequenz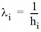 
der Linie abgeleitet. Der Begriff „Rest“ soll verdeutlichen, dass es um die verbleibende Reisezeit vom aktuell betrachteten Halt zum Zielbezirk geht. Nur bei der Wahlsituation am Quellbezirk handelt es sich um die Reisezeit des ganzen Wegs.
Zum Zwecke einer einfacheren Darstellung nehmen wir ferner an, dass die Linien aufsteigend nach ihrer Rest-Reisezeit sortiert sind, also gilt s1 ≤ s2 ≤ ... ≤ sn. Die Menge der ersten i Linien kürzen wir wie folgt ab: Li = {1, ..., i}.
Es sei angemerkt, dass die Rest-Reisezeit si in Wirklichkeit für die generalisierten Kosten der Linie i steht, darin sind Umsteigezuschläge und weitere Widerstands-Komponenten enthalten. Zum besseren Verständnis sprechen wir im Folgenden aber dennoch nur von „Zeiten”.
Die verschiedenen Wahlmodelle ermitteln die auf der Basis der verfügbaren Informationen optimale Menge L* ⊆L und für jede Linie i ∈ L* einen Anteil πi ≥ 0 an der Nachfrage.
Es ist intuitiv klar, dass eine Linie i Teil von L* sein muss, wenn eine andere Linie j in L* enthalten ist, und für die Rest-Reisezeiten si < sj gilt. Aus der Sortierung der Zeiten folgt somit, dass ein i* existiert, sodass L* = Li*.
Die Wartezeit, die sich bei Wahl einer beliebigen Menge L‘ vor dem Einstieg ergibt, bezeichnen wir mit WL‘. Die zugehörigen Restkosten sind folgendermaßen gegeben.
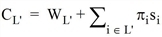
Die Größen sind Zufallsvariablen, weil sie vom zufälligen Eintreffen der Linien an der Haltestelle abhängen.
Für die optimale Menge L* gilt also E(CL*) ≤ E(CL‘) für beliebige L‘ ⊆L.
